Сводка основных формулЗанятие № 5 |
|
|
1. Матрица-корреспонденция
|
|
|
2. Матрица-проводка
Может быть неокаймленной, то есть без итогов, или окаймленной. Например,
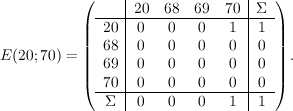
Она же окаймленная:
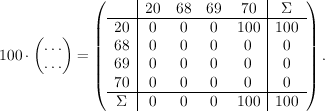
При умножении получаем матрицу с итогами:
|
|
|
3. Матрица операций— это формула журнала операций |
|
|
|
|
|
|
4. Матрица дебетовых оборотов— это матрица сводных проводок, полученная приведением подобных в формуле журнала операций.
|
|
|
где |
|
|
5. Основное уравнение бухгалтерского учета
В результате умножения обеих частей на вектор формирования итогов получаем |
|
|
6. Векторно-матричные формулы балансовых отчетов |
|
|
— симметричная главная книга.
— левосторонняя главная книга, применяемая сегодня в практике учета.
— правосторонняя главная книга.
— уравнение оборотно-сальдового баланса, где
|
|
|
7. Векторы дебетовых и кредитовых оборотовполучаются преобразованием соответствующих формул:
— формула вектора дебетовых оборотов, где
— формула вектора кредитовых оборотов, где |


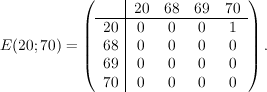
![\underbrace{\text{МС}_{t-1}}_{\mbox{\parbox[t]{1.6cm}{\centering матрица\ сальдо\ на~начало\ периода}}} + \;\text{МДО} - \text{МКО} \;= \underbrace{\text{МС}_t}_{\mbox{\parbox[t]{1.6cm}{\centering матрица\ сальдо\ на~конец\ периода}}}\;](/smm/i/tex/173362411c3ca48e45fd77e7a312990a.png)