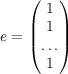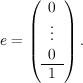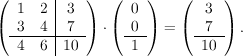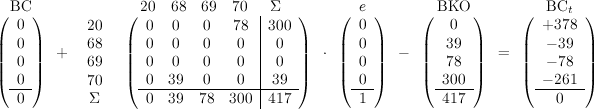Матричная модель бухгалтерского учета и формирования балансовой отчетностиЗанятие № 4 |
|
|
Бухгалтерский учет как объект математического моделирования рассматривался такими российскими авторами, как Руссиян, Попов, Колпотин, Шерр, Рудановский, Блатов, Вейцман. Впервые задачу представления бухгалтерского учета в виде уравнений сформулировал итальянский профессор информатики Ломбарди в 1967 г.: |
|
|
1. Задача бухгалтерского учета известна только в терминах ее процедуры. 2. Легко составить блок-схему любой задачи, так как блок-схема только отражает ее шаги. 3. Необходимо найти способ определения такой задачи в компактном виде, подобном описаниям математической задачи, посредством уравнения. |
Цитата из Ломбарди. |
|
|
История науки показывает, что не всегда связь в виде математического уравнения может быть установлена сразу и непосредственно. Например, долгое время процедуры решения систем линейных уравнений не были представлены в виде уравнения, содержащего решения. |
|
|
И только средствами матричной алгебры удалось записать СЛУ в виде матричной алгебры: |
|
|
|
|
|
Аналогичное положение имеет место в бухгалтерском учете. |
|
|
Построение матричной модели бухгалтерского учета сводится к следующим шагам: 1) первичным записям-проводкам ставятся в соответствие их эквивалентные образы в виде матриц; 2) операциям по преобразованию данных ставятся в соответствие их эквиваленты в системе матричной алгебры; 3) связь входящих и исходящих сальдо устанавливается с помощью матричного уравнения (основного уравнения бухгалтерского учета в матричной форме); 4) преобразование основных уравнений позволяет найти формулы для решения задачи формирования балансовых отчетов в системе матричной алгебры; 5) эти матричные формулы являются эквивалентами связей и показателей, представленных в таблицах балансовых отчетов. |
|
|
Основные определения матричной модели |
|
|
Бухгалтерский учет решает две основные задачи: 1. Формирует первичные записи. 2. Преобразует эти записи в балансовый отчет. Введем в основу рассматриваемой системы два основных определения: |
|
|
1. Матрица-корреспонденция — это квадратная матрица, определенная на плане счетов, в которой на пересечении дебета и кредита находится единица, а остальные элементы равны нулю. Обозначается E(X; Y), где X и Y принадлежат множеству счетов. 2. Матрица-проводка — это произведение суммы операции на матрицу-корреспонденцию.
|
|
|
Здесь и далее первый символ в аббревиатуре M обозначает матрицы, B — векторы. Пример: Дт 50, Кт 51 — 1000 д.е.
|
|
|
Журнал операций: |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
После приведения подобных получаем матрицу дебетовых оборотов |
|
|
|
|
|
Связь между входящими и исходящими остатками устанавливается с помощью основного уравнения бухгалтерского учета: |
|
|
|
|
|
В нашем примере:
Получение балансового отчета на основе математической модели осуществляется путем элементарного преобразования — умножения обеих частей на вектор формирования итогов:
Пример: |
|
|
Для окаймленных матриц: |
Окаймленными называются матрицы с итогами. |
|
|
Пример: |
|
|
|
В нашем примере — 10. |
|
|
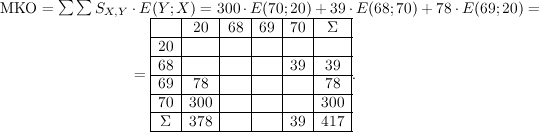
Таким образом,
где
|
|
|
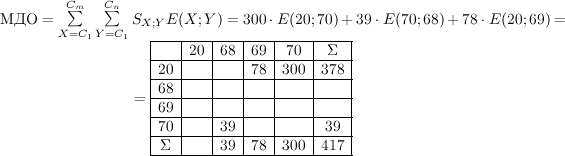
Запишем по данным нашего примера главную книгу:
Это — алгебраическое представление главной книги. |
|
|
|
|
|
Бухгалтерская запись главной книги: |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|


![M(50; 51) =
100~\cdot\quad
\underbrace{\begin{array}{c|cccccc|}
\mbox{Д}\backslash\mbox{К} & 01 & \ldots & 50 & 51 & \ldots & 99 \\hline
01 & & & & \vdots & & \
\ldots & & & & \vdots & & \
50 & \hdotsfor[2]{3} & 1 & & \
51 & & & & & & \
\ldots & & & & & & \
99 & & & & & & \
\end{array}}_{\mbox{МК}}
=
\underbrace{\begin{array}{c|cccccc|}
\mbox{Д}\backslash\mbox{К} & 01 & \ldots & 50 & 51 & \ldots & 99 \\hline
01 & & & & \vdots & & \
\ldots & & & & \vdots & & \
50 & \hdotsfor[2]{3} & 100 & & \
51 & & & & & & \
\ldots & & & & & & \
99 & & & & & & \
\end{array}}_{\mbox{МП}}](/smm/i/tex/1141a29d667e05ca5149eafb70d5dbd7.png)
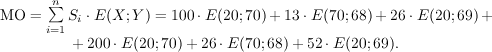
![\underbrace{\text{МС}_{t-1}}_{\mbox{\parbox[t]{1.6cm}{\centering матрица\ сальдо\ на~начало\ периода}}} + \underbrace{\text{МДО}_{t-1, t}}_{\mbox{\parbox[t]{1.6cm}{\centering матрица\ дебетовых\ оборотов}}}\; - \text{ МКО}_{t-1, t} = \text{МС}_t](/smm/i/tex/eb712b7f30f96ae74cd6eef325f44f8a.png)